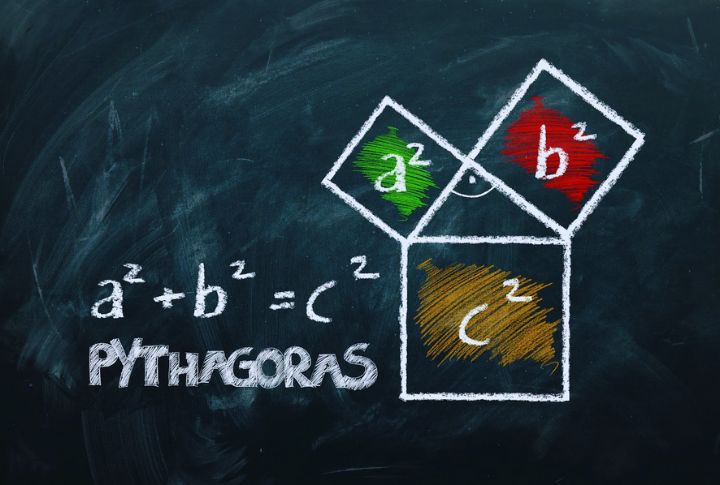
We live in a world built on hidden formulas we don’t always see. These include complexities like ancient geometry and quantum economics, where numbers have held secrets that were way ahead of their time. While some theories just filled up chalkboards, others flipped our understanding of reality. Here are 10 of those revolutionary ideas.
Infinity And Set Theory (Cantor)
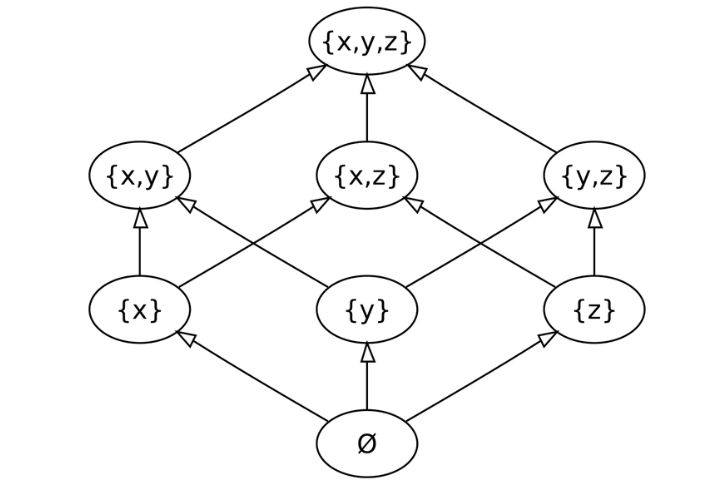
Can one infinity be bigger than another? It sounds strange, but Cantor showed it’s true. By comparing different sets, he proved that some infinities, like real numbers, are larger than others, like integers. This revelation completely reshaped the way we think about math and logic. Now, we understand that infinity isn’t just endless—it’s layered and more complex than we ever imagined.
Pythagorean Theorem
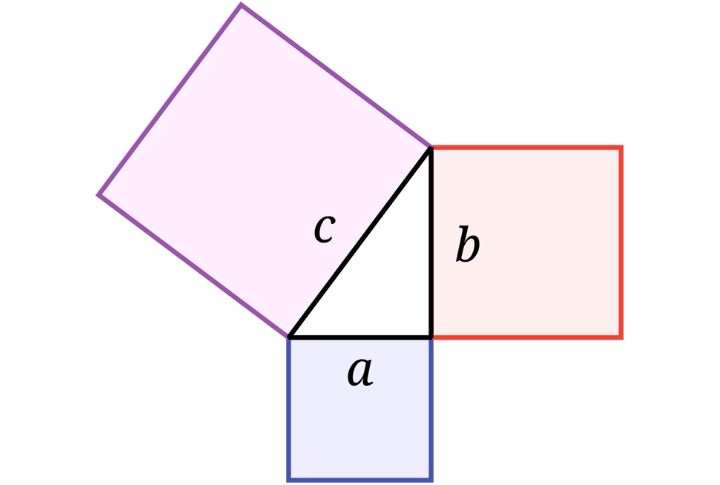
Early builders discovered right angles long before proofs by stretching ropes tight between stakes. Then came the Greeks. You learned it as a² + b² = c², but this ancient principle powered cathedrals and coded GPS, among many other things. Its triangle still shines through architecture, engineering, music, and algorithms.
Calculus (Newton And Leibniz)

You drop an apple, and it falls quickly. But how fast, precisely, right at this second? That’s where calculus comes in. Developed independently by Newton and Leibniz, it unlocked the math of change. Suddenly, scientists could measure and model things like motion with precision. This breakthrough transformed our understanding of gravity, electricity, and how everything moves.
Prime Number Theorem
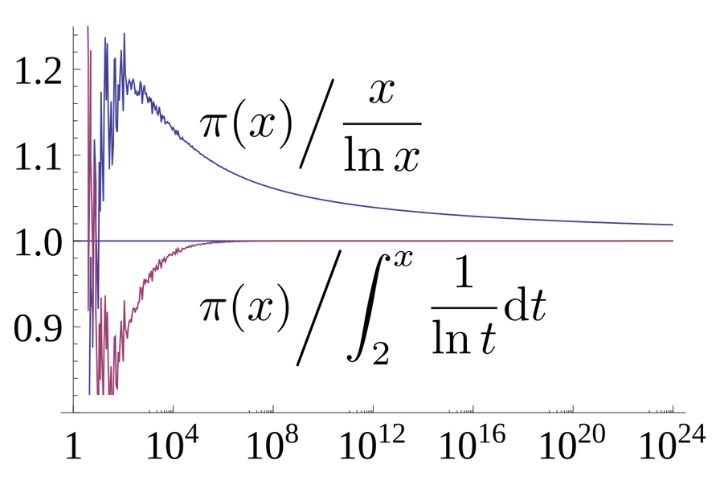
Primes don’t appear in order. They feel random, but as numbers stretch toward infinity, primes begin to follow a pattern in density. The Prime Number Theorem reveals how they thin out predictably. Of course, it doesn’t list them, but it forecasts their frequency. It turns out prime chaos has a rhythm.
Godel’s Incompleteness Theorems
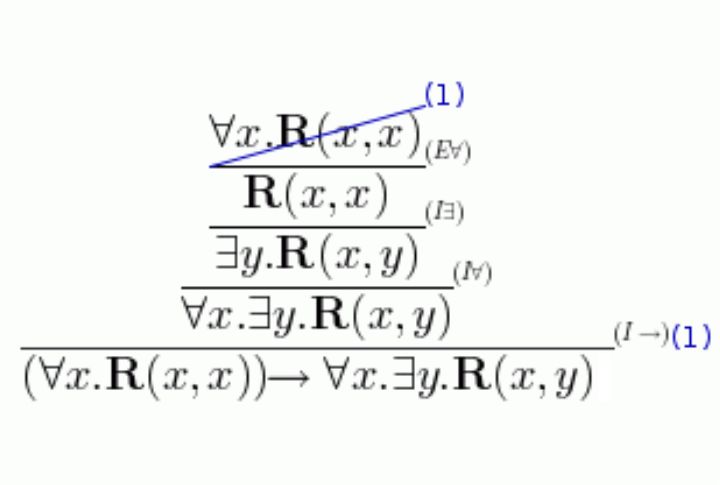
You rely on systems to work, but can they prove themselves? Godel showed that no complete mathematical system can fully validate its own truths. Sounds unsettling, right? Even logic has its limits. With one groundbreaking theorem, he shattered the dream of total certainty and exposed cracks in every formal system.
Chaos Theory

A butterfly flaps its wings. Weeks later, a storm forms. That metaphor lives inside chaos theory, where tiny differences in input cause massive, unpredictable changes in outcome. Weather, relationships, ecosystems, and even stock markets fall under its spell. Math, once thought predictable, now plays to hidden rhythms with uncertainty.
Game Theory (Nash Equilibrium)
You’re playing a game, and so are others. Your best move depends on theirs—and vice versa. Nash formalized this circular dance in his equilibrium theory, and decisions became math, from economics to dating. It changed how governments negotiate and how businesses price. The world has become a strategy board and everyone’s playing.
Fermat’s Last Theorem

Fermat scribbled a note claiming a proof too large for the margin. For centuries, no one could find it. His claim: no three whole numbers satisfy aⁿ + bⁿ = cⁿ for n > 2. It was solved only in 1994, but before that, it tested math’s limits and patience, pushing mathematicians to the brink of frustration and sparking countless failed attempts.
The Four Color Theorem
It seems straightforward: Color a map so that no adjacent regions share the same color. Four colors are all you need. But proving this took decades of attempts and, eventually, computer verification. This was the first central theorem to be proved by a machine. The simple task of coloring maps hid the surprising complexity of the problem beneath the surface.
Turing’s Theory Of Computability
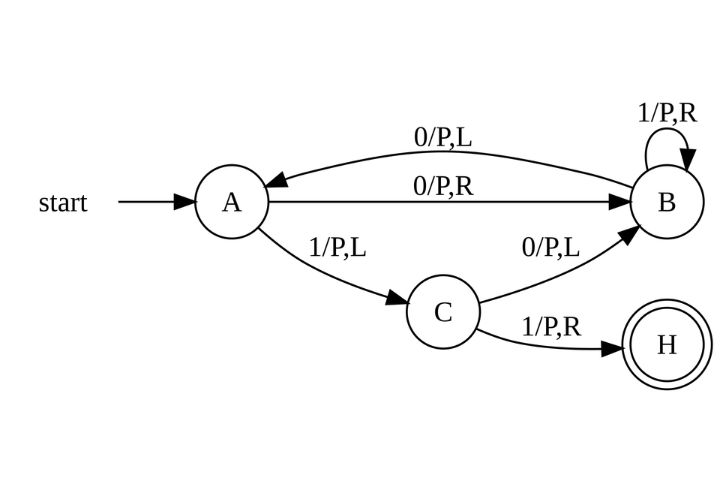
What if you face a problem and no method can solve it—ever? Turing showed that some questions are fundamentally unsolvable. His imaginary machine mapped the limits of logic itself. That breakthrough birthed computer science and went on to reveal math’s boundaries with chilling precision while altering what machines could mean.

